Diese Seiten wurden für den Girls' Day 2022 von Matthias Bartelmann, Fabio D'Ambrosio, Iris Feldt, Eileen Giesel, Lavinia Heisenberg, David Maibach, Sara Marcos Plaza, Nadine Nussbaumer, Alexander Oestreicher, Adrian Schirra, Sofía Vidal, Ricardo Waibel und Stefan Zentarra ausgedacht, geplant und umgesetzt, basierend auf dem Girls' Day 2021 Programm. Dabei entstand auch dieses Video, das unsere Arbeit erklärt.
Der Kosmische Mikrowellenhintergrund und Kugelflächenfunktionen
1) Die Weltkarte
Hier siehst du rechts eine Karte der Erde. Die Farben stellen dar, wie viele Meter m über N.N. = Normal Null (Meeresspiegel) sich das Festland befindet.
Manche Regionen haben negative Werte - was bedeutet das?
Überrascht dich das Bild?
Was würde passieren, wenn man über den Rand der Karte rechts hinausgehen würde?
2) Rekonstruiere die Höhe der Erde
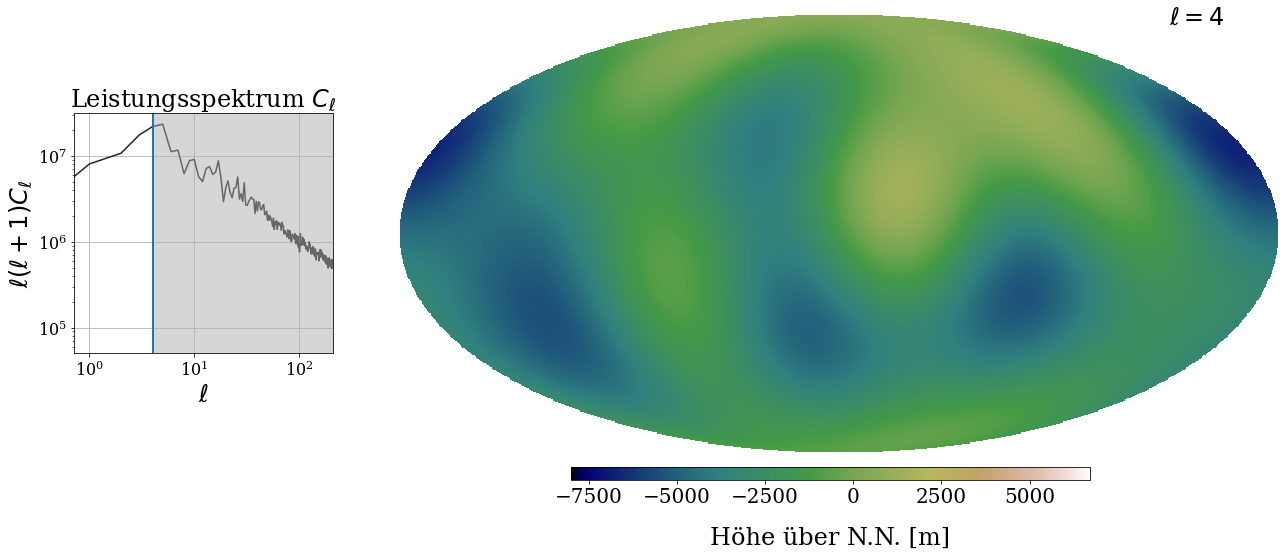
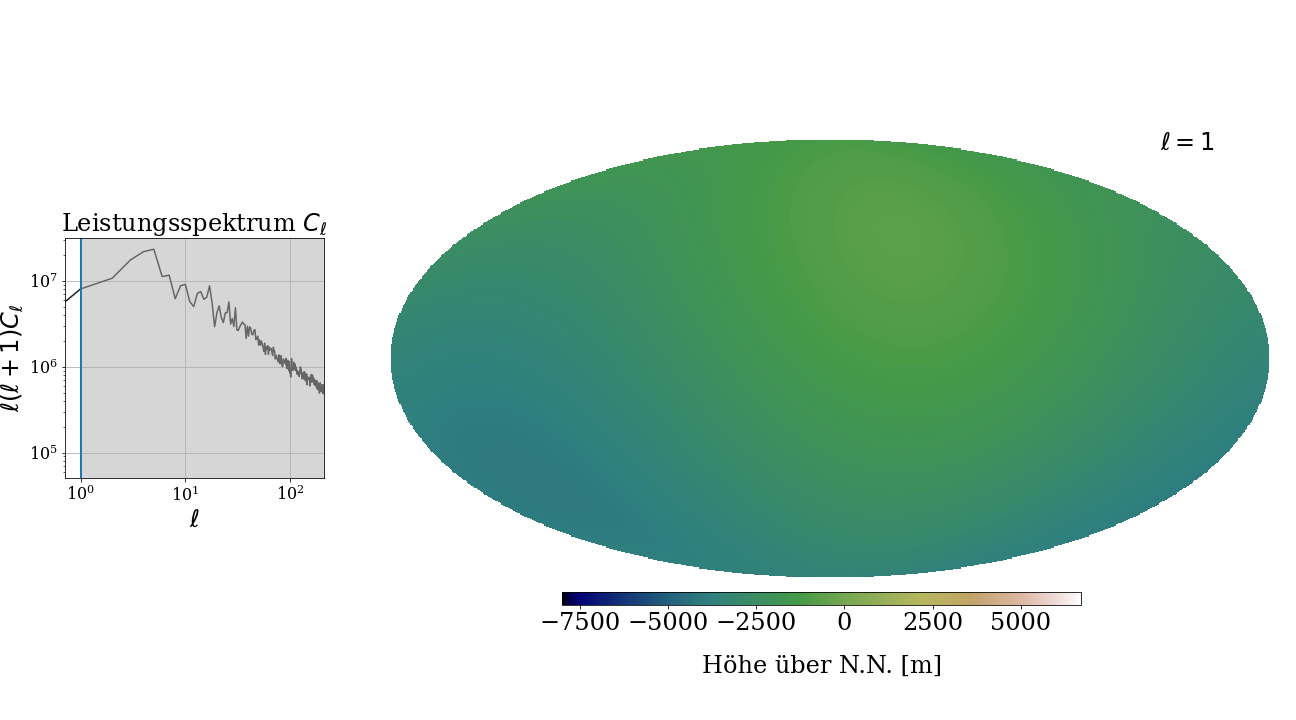
Rechts siehst du wieder die Erde - zumindest, wenn du den Regler mit ℓ ganz nach rechts schiebst.
Wie verändert sich das Bild der Erde, wenn du ℓ auf kleinere und größere Werte setzt?
Welche Rolle spielt das ℓ?
Links siehst du ein sogenanntes "Leistungsspektrum", mit dem wir auch in der Kosmologie arbeiten. Der weiße Teil stellt den Bereich dar, der zur Rekonstruktion des Bildes auf der rechten Seite benutzt wird. Ab der Skala ℓ, die du einstellst, wird der graue Teil ignoriert. Je mehr Information wir nutzen, um die Höhenfunktion auf der Erdoberfläche zu rekonstruieren, desto genauer können wir das Bild reproduzieren!
3) Wie funktioniert die Rekonstruktion? Was macht ℓ?
In der folgenden Grafik siehst du die Kugelflächenfunktionen. Wir nutzen sie für die Rekonstruktion. Wieso brauchen wir eigentlich Funktionen, die zweidimensional sind? Verstehst du, warum wir die Funktionen "Kugelflächenfunktionen" nennen? Warum "Kugel" und warum "Flächen"?
Für jedes ℓ (siehe Zeilen), gibt es eine oder mehrere "Basisfunktionen". Wie viele Basisfunktionen gibt es für ℓ = 1? Wie verändert sich das Aussehen der Basisfunktionen mit größerem ℓ?
Rechts siehst du, was passiert, wenn wir die Basisfunktionen mit einem Faktor gewichten (multiplizieren) und dann zusammenaddieren.
Du siehst wieder, je mehr Basisfunktionen (höheres ℓ) wir nutzen, desto genauer kann die Rekonstruktion werden.
… Doch woher wissen wir die Vorfaktoren von den Basisfunktionen? (siehe Teil 3b und 3c)

Hier kannst du selbst Basisfunktionen (mit richtigem Vorfaktor) zusammenaddieren und schauen, wie sich das Bild verändert.
3b) Woher wissen wir die Vorfaktoren?
Für ein eindimensionales Signal, sind Sinus-Funktionen die Entsprechungen von den "Kugelflächenfunktionen". In dem Bild siehst du solch eine Sinus-Funktion, mit zwei variablen Werten A und B. Verstelle einmal diese beiden Werte, was bedeuten / verändern sie?
Durch Überlagerung von verschiedenen Sinus-Funktionen können wir beliebige eindimensionale Signale erzeugen, wie zum Beispiel das Rote im folgenden Bild. Die blauen Sinus-Funktionen sind in diesem Spiel deine Basisfunktionen. Sie werden mit je einem Vorfaktor A, B und C multipliziert und zusammenaddiert. Das Ergebnis ist die schwarze Kurve. Kannst du die Vorfaktoren so einstellen, dass die schwarze Kurve das "gemessene" Signal reproduziert?
3c) Vorfaktoren in 2D?
Um wieder zurück zur Erde zu kommen, müssen wir wieder die Kugelflächenfunktionen betrachten anstelle der Sinus-Kurven. Unten links siehst du bereits teilweise aufsummierte Kugelflächenfunktionen, bei denen schon die errechneten Vorfaktoren verwendet worden sind. Übrig bleiben drei Bestandteile der Erde: die groben Strukturen (oben), die mittelgroßen Strukturen (mitte) und die feinen Strukturen (unten).
Kannst du die Vorfaktoren dieser drei Bestandteile so wählen, dass am Ende wieder unsere Erde rauskommt, wenn sie zum Bild rechts summiert werden?