Der Kosmische Mikrowellenhintergrund und Kugelflächenfunktionen
4) Kosmischer Mikrowellenhintergrund
Der CMB (= cosmic microwave background = kosmischer Mikrowellenhintergrund) ist Strahlung, die unsere Erde von allen Seiten erreicht.
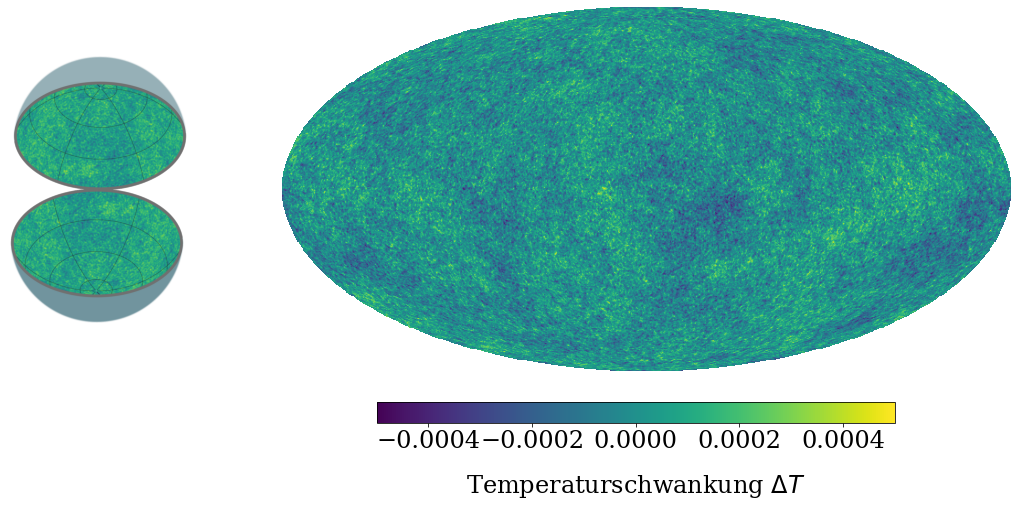
Du siehst links ein Bild, in dessen Mitte du dir die Erde oder unsere Galaxie vorstellen kannst. Schauen wir ins Weltall um uns herum, können wir eine zweidimensionale Karte erstellen, die den Mikrowellenhintergrund darstellt - genau wie bei der Erde.
Rechts siehst du diese Karte: Die Farben bedeuten hier Temperatorschwankungen Δ𝑇 zwischen etwa −0.0005K und +0.0005K. Diese werden in Kelvin K angegeben. Die Schwankungen sind um eine mittlere Temperatur von 2.73K.
Wie klein sind die Schwankungen im Verhältnis zum Mittelwert?
Kannst du Muster in dem Bild erkennen? Nein? Das können wir mit bloßem Auge auch nicht...
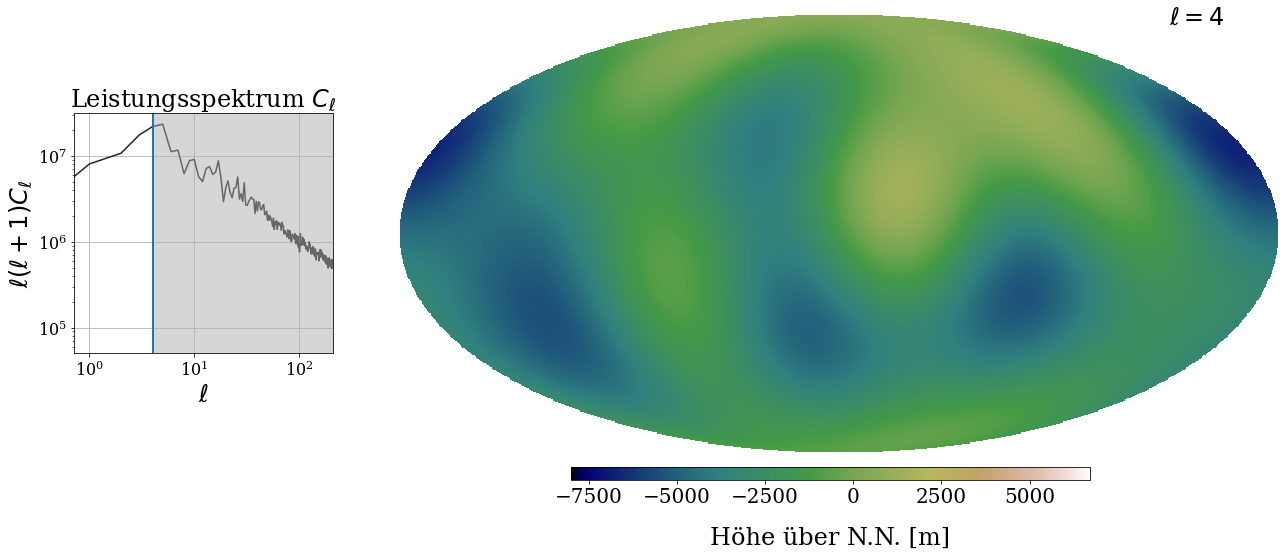
Hier kannst du wieder das Bild des CMB rekonstruieren, indem du den Regler mit ℓ verschiebst. Je größer ℓ ist, desto mehr Basisfunktionen mit richtigem Vorfaktoren addierst du zusammen. Das Bild wird also genauer.
Du siehst links wieder das "Leistungsspektrum" - nur, dass es diesmal völlig anders aussieht als bei der Erde! Es zeigt die Vorfaktoren passend zur entsprechenden Basisfunktion. Wenn du den Regler verschiebst, siehst du, dass mehr oder weniger Basisfunktionen genutzt werden, um den CMB zu rekonstruieren.
Je mehr Vorfaktoren wir bestimmen können, desto genauer können wir die Realität abbilden. Wir haben folglich mehr Information und können unsere theoretischen Vorhersagen besser mit den Beobachtungen vergleichen. Ein Beispiel siehst du in Teil 5.
5) Wie groß ist der Anteil der Atome im Unviersum?
Im Universum gibt es dunkle Materie und sichtbare Materie. Letztere besteht fast vollständig aus Atomen, also dem was wir kennen.
Wir können Berechnungen machen, um vorherzusagen, wie das Leistungssprektrum des CMB aussieht. Aber das hängt auch davon ab, wie groß der Anteil der Atome im Universum ist. Deswegen vergleichen wir unsere theoretischen Modelle mit den Beobachtungen und können so die fehlende Größe bestimmen.
In der Grafik siehst du in rot, wie das beobachtete Leistungsspektrum aussieht. Wenn du den Regler verstellst, ändert sich der Anteil der Atome im Universum. Du siehst in schwarz, was unser Modell für das Leistungsspektrum vorhersagen würde.
Wann stimmt unser Modell mit der Beobachtung überein? Kannst du rausfinden, wie groß der Anteil der Atome im Universum ist?
Quellen: Die verwendeten Daten der Erde stammen von dem ETOPO5-Projekt, die CMB Daten von der ESA und der Planck-Kollaboration. Die Grafiken wurde mit Python erzeugt, hauptsächlich mit den Bibliotheken matplotlib, healpy, cartopy, astropy und camb.